Gaming Life: Agency and Temporality in Early Cyberculture
The Game of Life (GOL) is an algorithm invented by the mathematician John Conway in the late 1960s that anticipates key aspects of cyberpunk: both cyberpunk and the GOL posit versions of life sustained/contained within mechanical systems, a visual aesthetic of precisely gridded space and a fascination with the games that might take place within such a space. They also share a science fictional lexicon: Conway claims he was inspired to create the GOL after learning of John Von Neumann’s efforts to imagine a Mars terraforming machine that could build copies of itself. The GOL’s terminology reflects this, with cellular “spaceships” that can travel at up to half the “speed of light.”
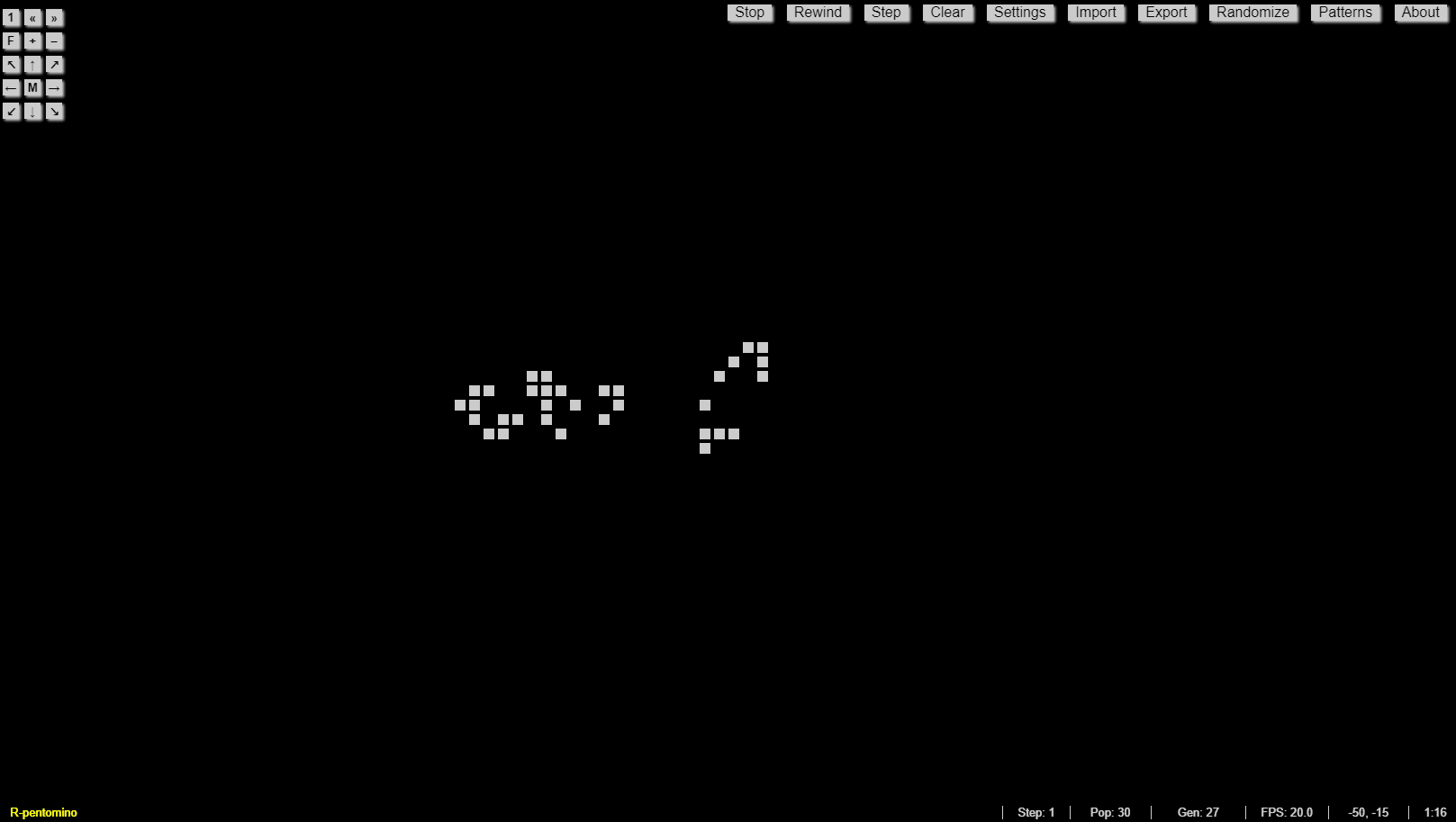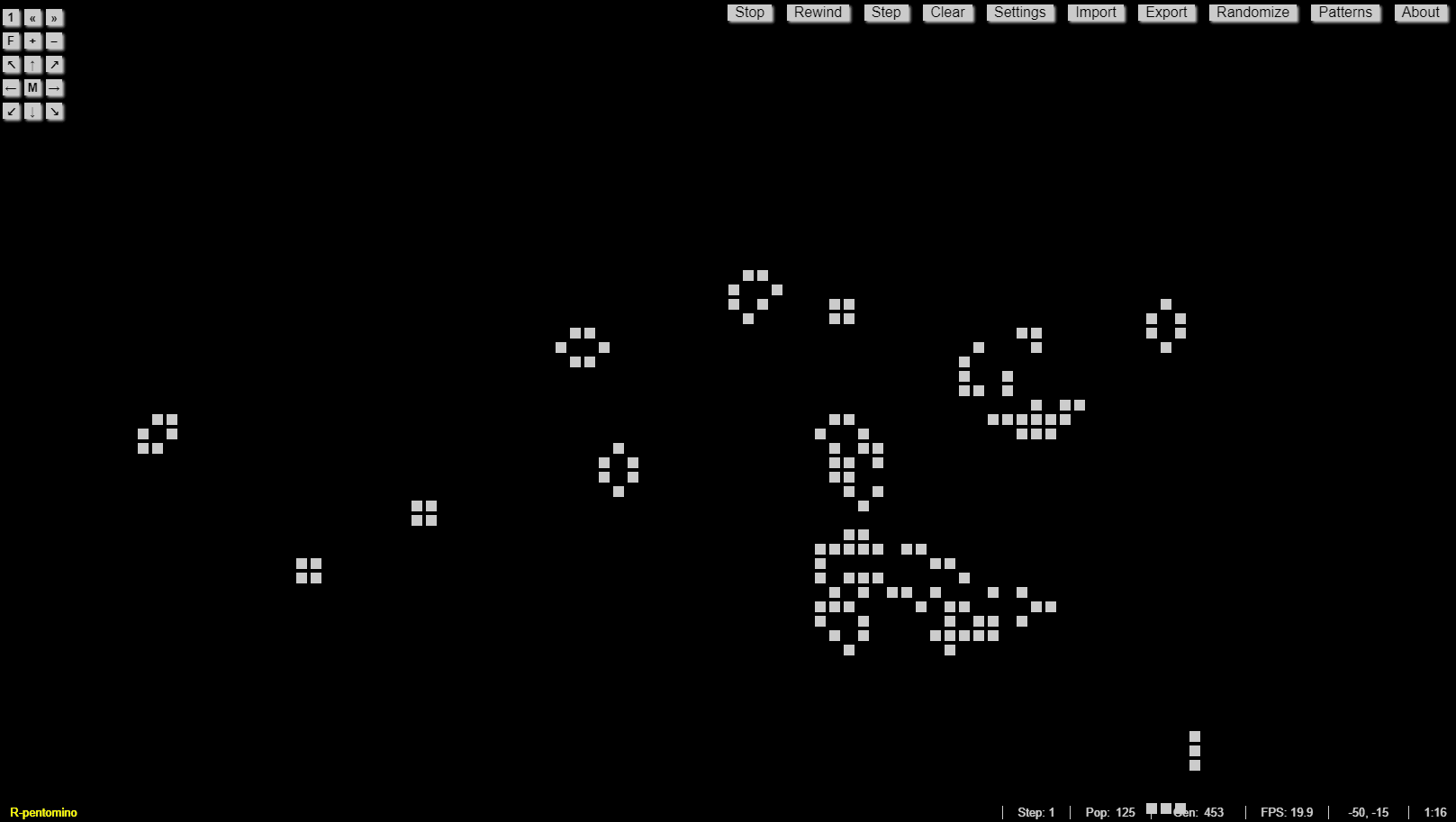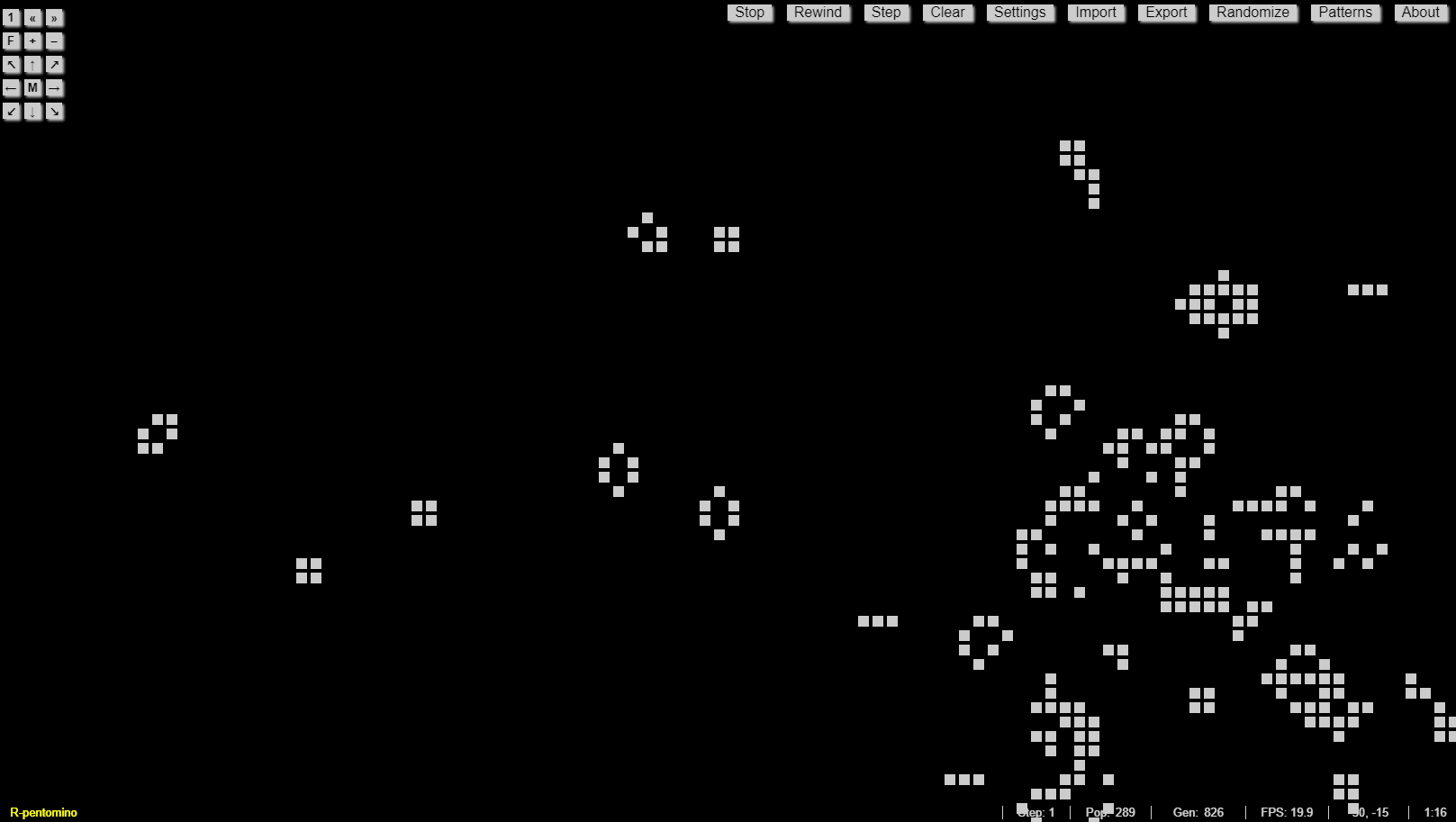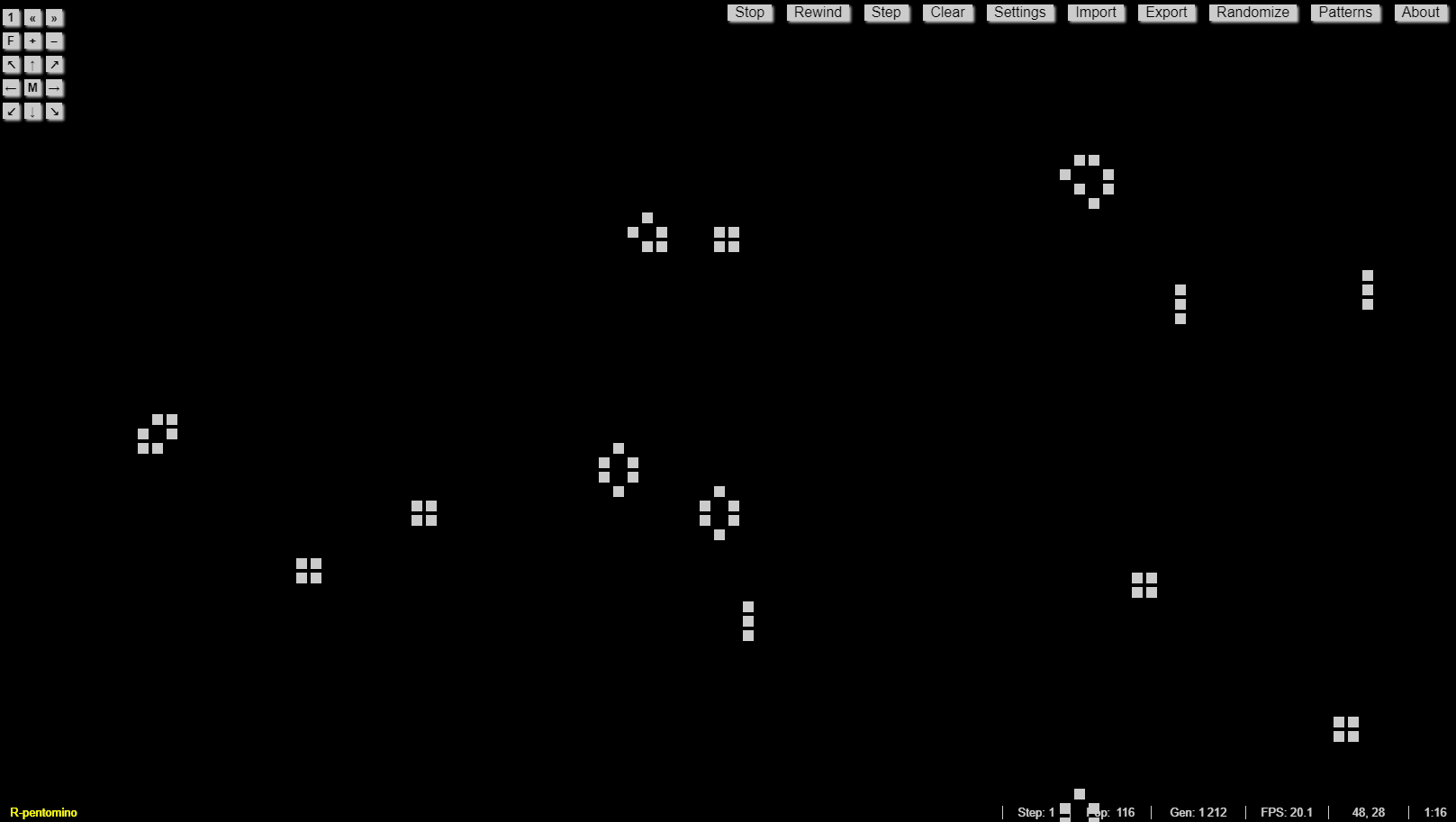
Recent scholarship suggests that cyberpunk is more than a subgenre: it has become a form for reflecting the conditions of late capitalism. In this vein, we are interested in exploring the GOL as one of the first technologies that articulated the idea of “life” within a cybersystem. Perhaps this exploration can point to potentialities and limitations of cyberspace that deserve further attention. In this work, we follow on analyses done by N. Katherine Hayles, Stephan Helmreich, and Colin Milburn, each of whom has written on the relationship between cellular automata research and science fiction, showing how the latter shapes the interpretations and aims of the former. Our contribution to this conversation is to interrogate the differences among simulation, game, and model as expressions of “digital life.” In these differences lies a question of control and of scale that is also important to cyberpunk: in a system of total capture, what agency is possible? Is one playing within a set of rules, or is any agent merely part of the rules of the system?
In 1970, Martin Gardner first introduced the Game of Life to the public in his monthly “Mathematical Games” column in Scientific American: “Because of its analogies with the rise, fall and alterations of a society of living organisms, [the game of life] belongs to a growing class of what are called ‘simulation games’– games that resemble real-life processes” (Gardner 1970, 121). The GOL, as you can see in the images here, is a simple grid– whether digital, implemented on graph paper, or on a game board– that has been overlaid with small dots, or counters. So where and how does “life” get into the Game of Life, and in what ways does it, as Gardner asserts, “resemble real-life processes?”
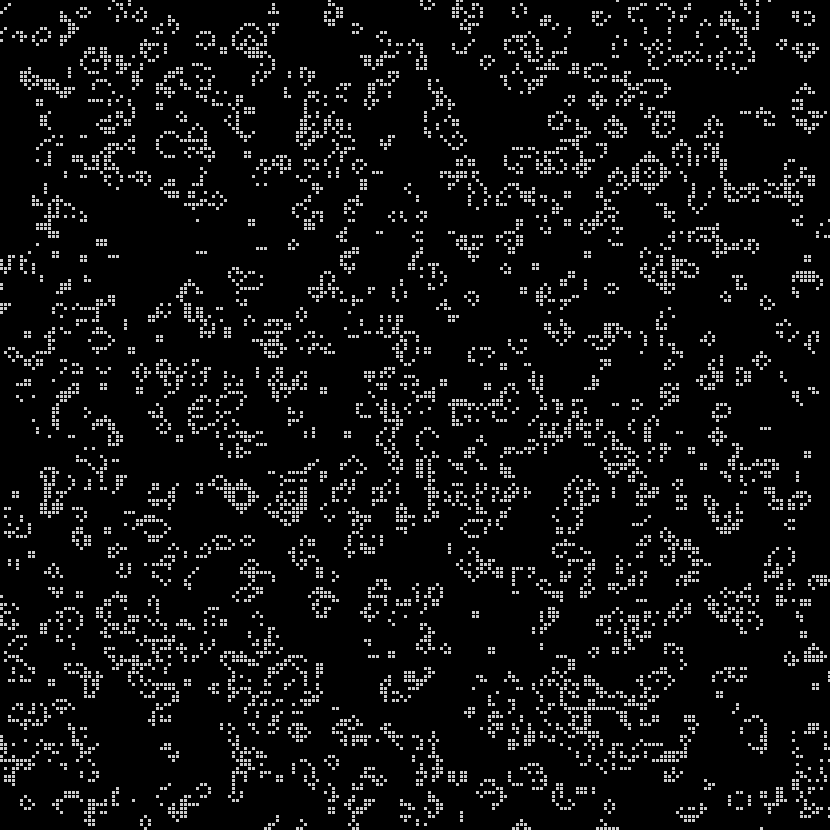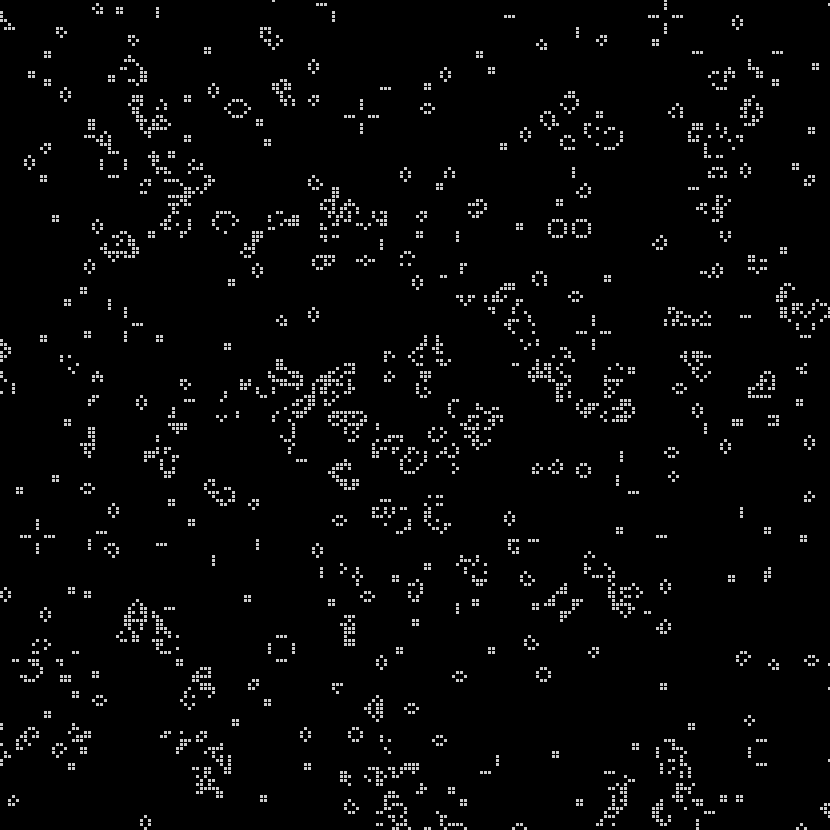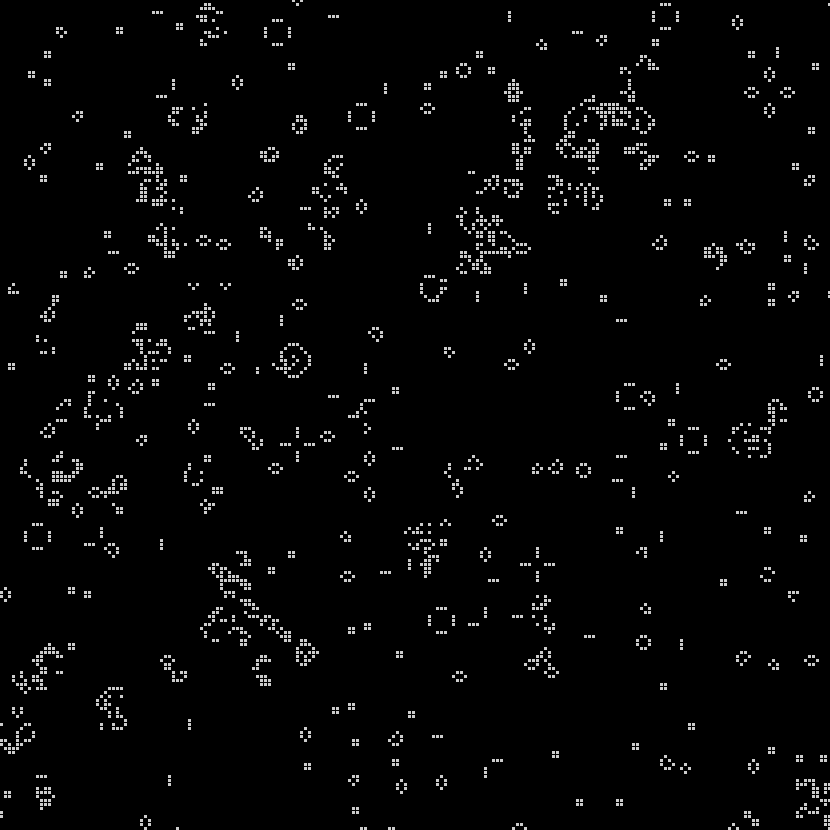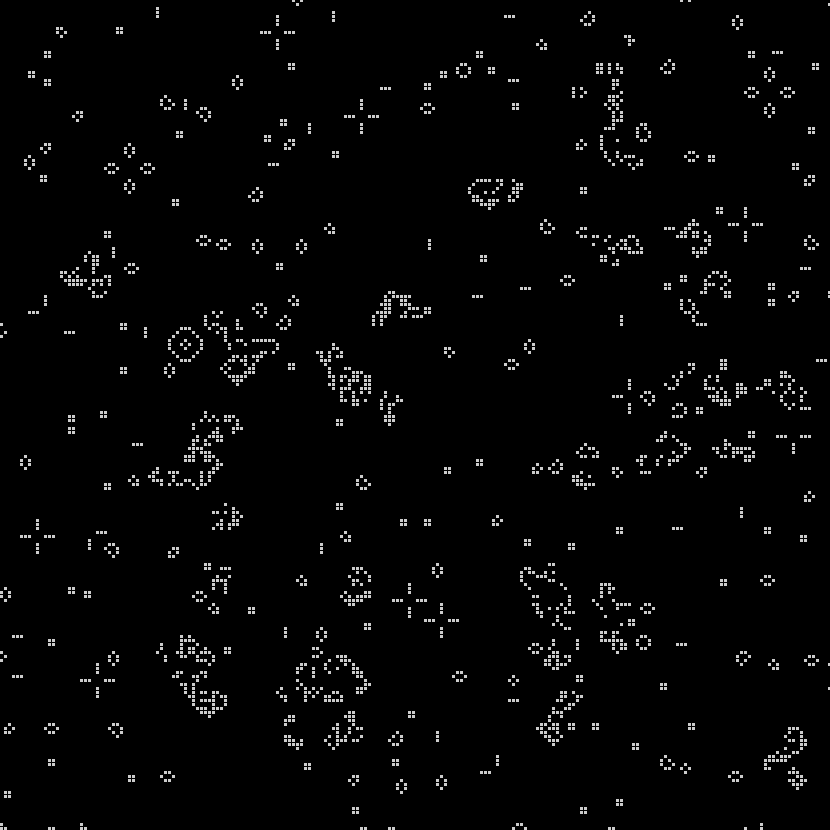
A strangely mixed set of ‘life’ metaphors, some incompatible with one another, give the GOL the flavor of a living system. In the original Scientific American column, Gardner instructs would-be players: “The basic idea is to start with a simple configuration of counters (organisms), one to a cell, then observe how it changes as you apply Conway’s ‘genetic laws’ for births, deaths and survivals” (120). This articulation is at pains to substitute organic metaphors for terms that would otherwise pertain to board games– “counters” are parenthetically denoted as “organisms,” while the game’s rules become “genetic laws for births, deaths and survivals.” On the game’s grid, a “single generation or, as we shall call it, a ‘move’ in the complete ‘life history’ of the initial configuration” is advanced by assessing the number of “neighbors” each cell has in the eight surrounding squares. Reflecting early 1970s environmentalism and the burgeoning fear of overpopulation, the main determinant of survival is population-related: “each counter with four or more neighbors dies (is removed) from overpopulation. Every counter with one neighbor or none dies from isolation” (120-1).
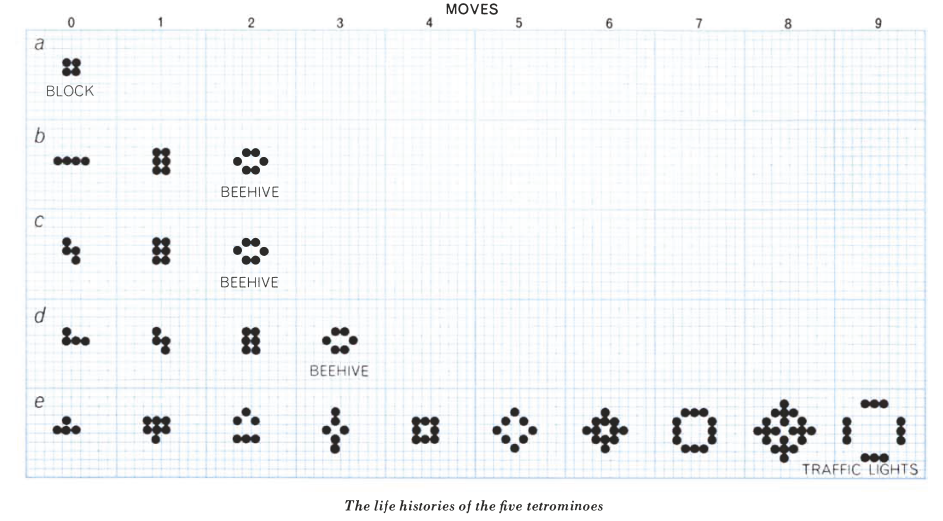
The incompatible metaphors of overpopulation and ‘genetic laws’ correspond to two approaches to “life” that take place at different hierarchical levels of complexity. At one level, the GOL’s field is a seething space of population interactions, with each cell as an individual organism subject to birth, death or survival. At another level, Conway and the many recreational mathematics researchers who responded to Gardner’s column were quick to develop taxonomies and species of entities within the GOL. Thus we see “pulsars” and “traffic lights,” “beehives” and “honey farms.” These entities are forms rather than individuals, each one made up of a configuration of cells.
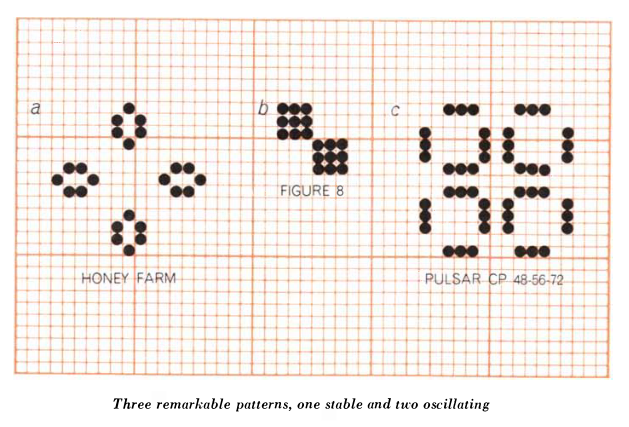
At a final, higher level of organization we find a kind of pattern within the GOL that was only hoped for at the game’s introduction in 1970: one that satisfies Conway’s interest, following Von Neumann’s terraforming ambitions, in finding a “pattern that [can] grow without limit” (120). Such a pattern, in this case a “glider gun” that expels spaceships indefinitely, was finally identified by some of Gardner’s readers at MIT the following year (Gardner 1971). The discovery of the glider gun implied that the GOL was Turing complete: it was possible to make any computation from within the game itself.

Collective understanding of the possibilities in the GOL also progressed in stages, as we discovered by playing the game the way it was invented. The material emergence of the game itself was not mathematically inevitable, but a historical result of Conway’s efforts to create a ruleset for cellular automata that would maximize unpredictability. To find the perfect balance of deaths, births, and survivals, Conway spent years with colleagues and students tinkering with different iterations of the rules on a go board (go is a Chinese strategy game akin to chess).
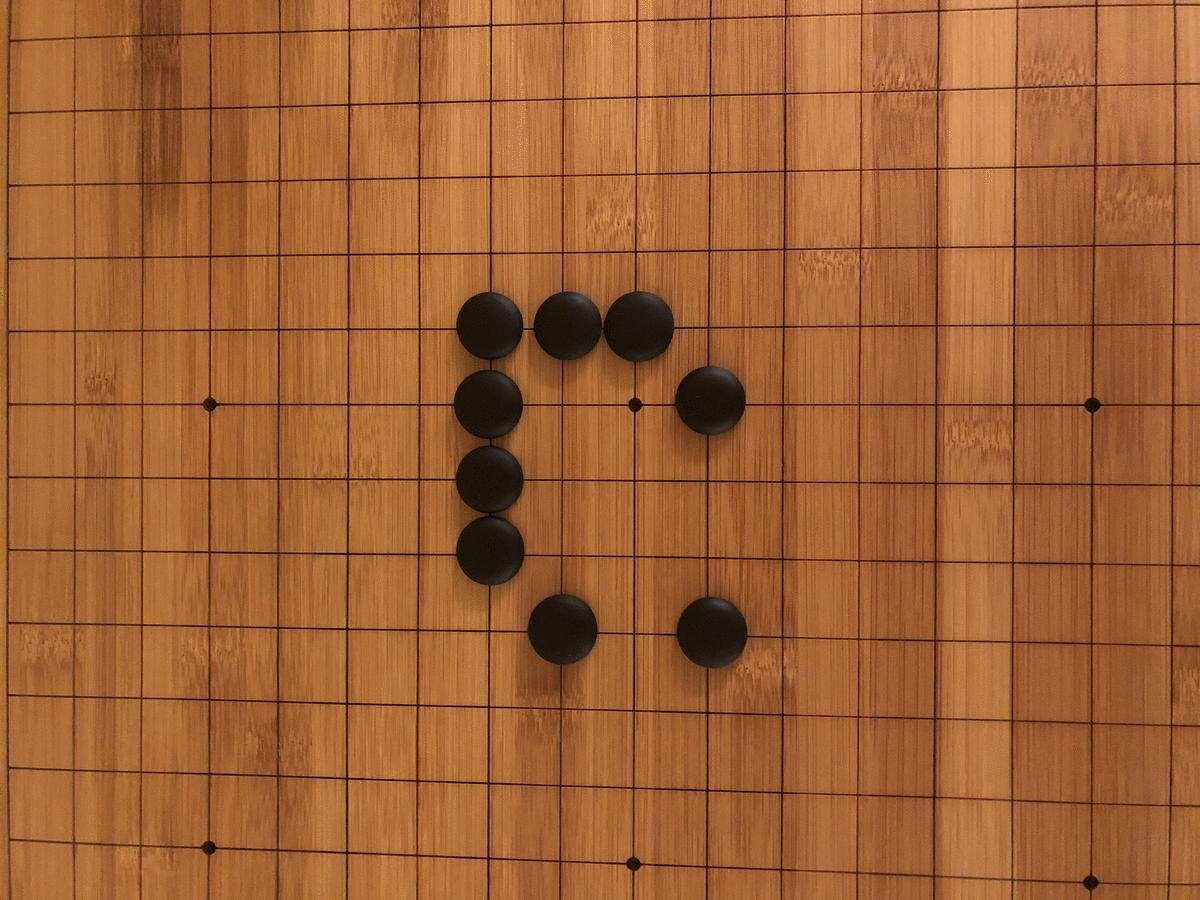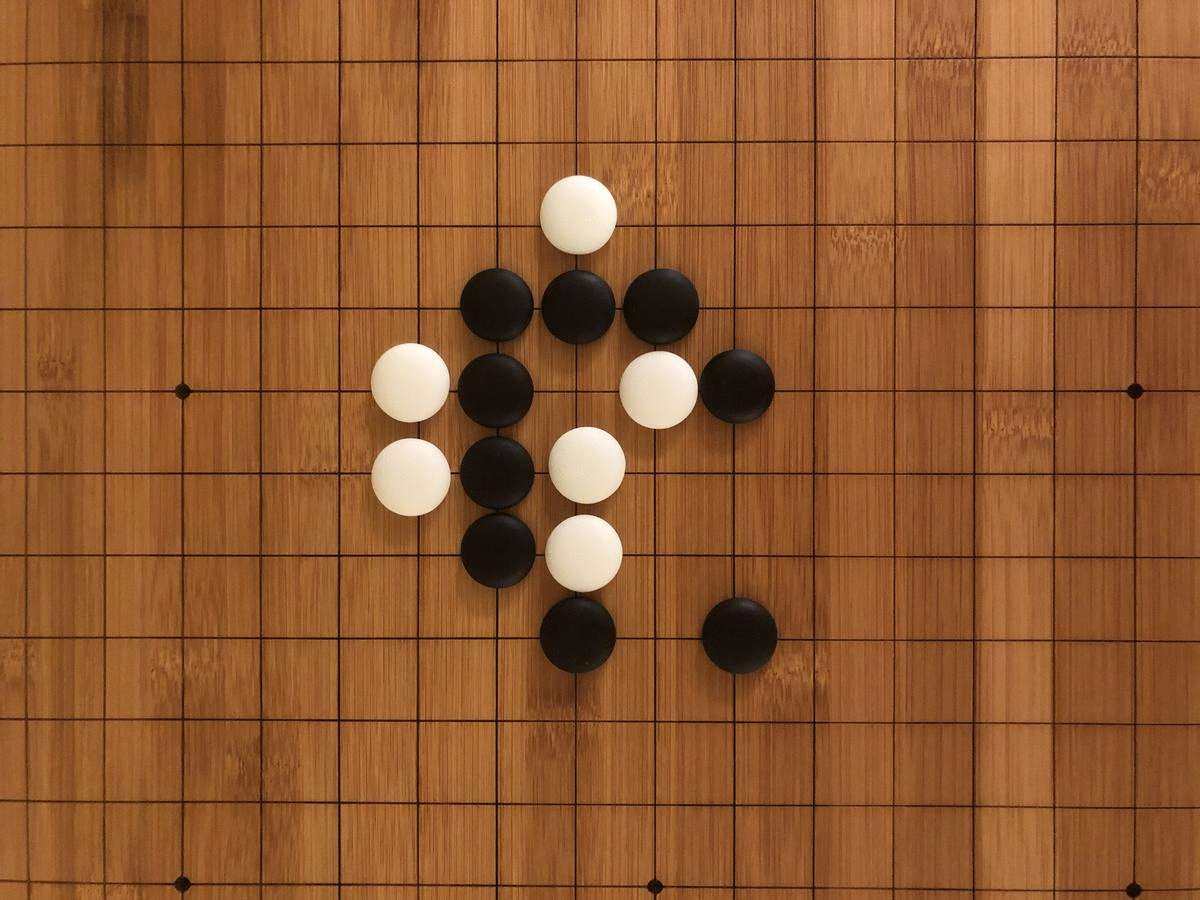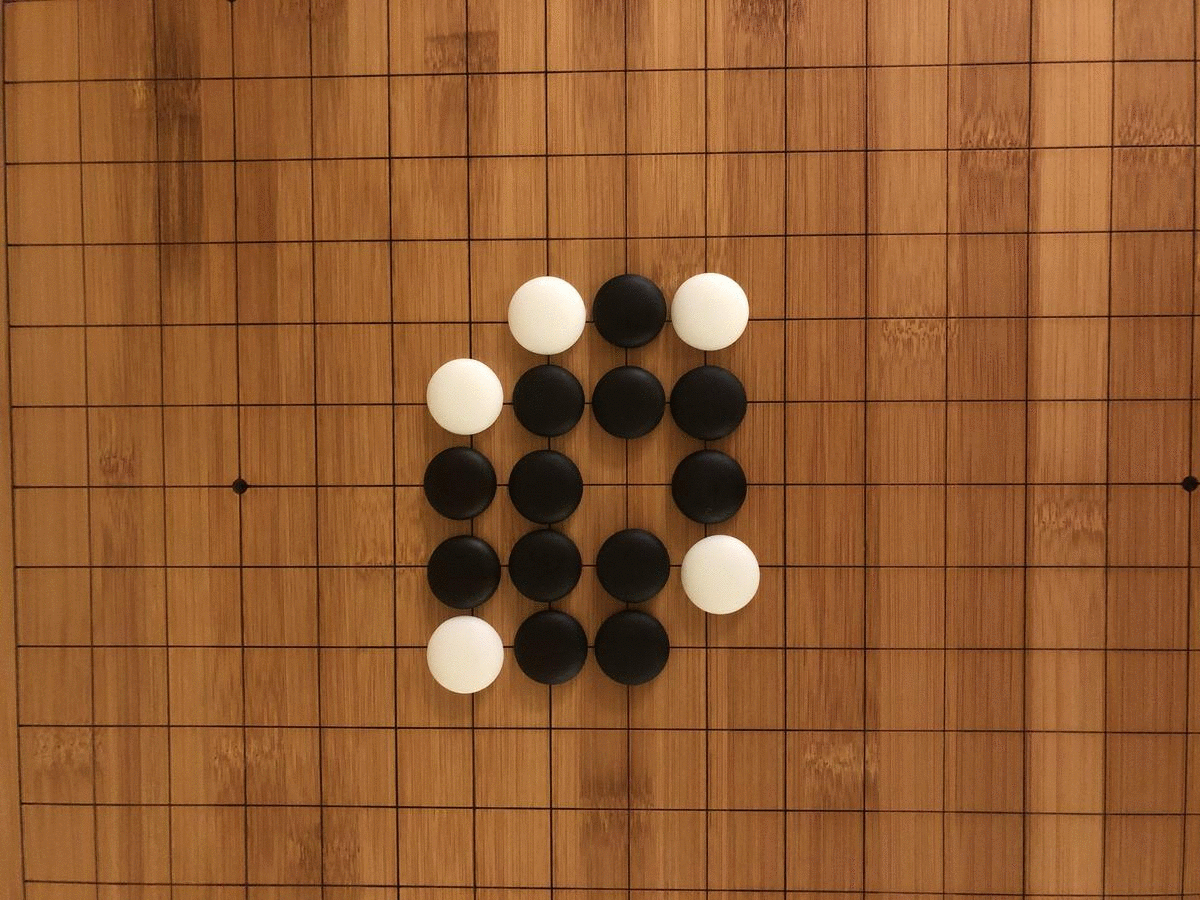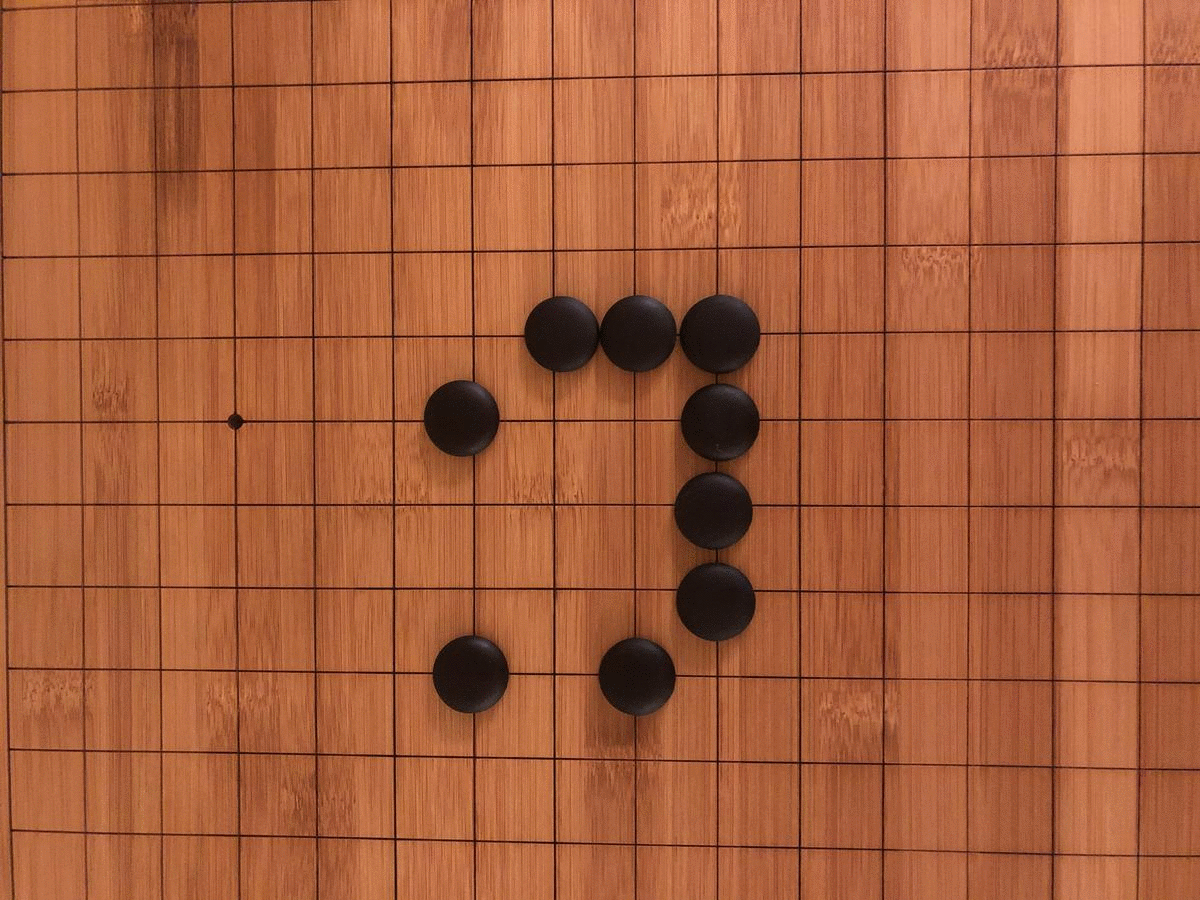
When we played the GOL on a go board ourselves, we realized how limited the game was without computational help. The need to mentally track each transformation before progressing to the next turn led to frequent errors and monotonous calculations. Our perception of time was focused less on a succession of turns and more on a series of sub-turns. Each segment of the board had to be separately calculated twice (once for births and once for deaths) with painstaking care to avoid double-counting. There were also material limitations preventing our discovery of an emergent pattern like the glider gun. Even a modestly scaled Game of Life grid of 200×200 over 2000 iterations would require 100 go boards tiled across a conference room, with each turn taking upwards of an hour. Under such conditions, it would be difficult to notice even a “flip flop,” as GOL enthusiasts call a blinking, two-state stable condition.

The discoveries now synonymous with the GOL were therefore reliant on the ability of experimenters to shift scale in space and time. This was first made possible by Guy and Bourne’s PDP-7 computer program, written shortly before Gardner’s column was published.

The invention of the original GOL algorithm by Conway and his colleagues, through hands-on tinkering, led to the eventual discovery of the glider gun by experimenters playing with visualization software, and then to software written to test thousands of starting configurations automatically. Years of such collaborative scaffolding led to the construction of a Universal Turing Machine and even a higher-order Game of Life emulator within the GOL, both aided by the development of layers of software and practice that assisted in the construction of such emergent structures.
Each stage in the growing complexity of the GOL reaffirms the principle that what gives “life” to the Game of Life is the painstaking labor of the biotic organisms in the cybernetic circuit of computational research. And the innovations and discoveries that characterize our understanding of the Game of Life today are themselves the result of treating the GOL not just as a model or simulation, but as a game, by exploring the open-ended possibilities of a simple algorithm as a form of play.
The oscillating definition of the GOL between model and game has consequences not just for its role in Artificial Life research, but also for how agency in cybersystems is understood. To play with a system rather than merely playingin a system is to recognize the social relations that structure the emergence of cybersystems in the first place. Each new hierarchical layer of abstraction begins as a sandbox, and only later becomes a platform on which further play can be staged. In this light, the conceptual boundary between model and game seems to sell both categories short. After all, the game of life is an increasingly poor model of population growth even as it becomes a more fascinating site for knowledge production. Within the striated matrices of cyberspace, play finds its own uses for models.
WORKS CITED:
- Bradbury, Philip. “Life in life,” May 13, 2012. Online. https://www.youtube.com/watch?v=xP5-iIeKXE8.
- Gardner, M. (1971). Mathematical Games: On cellular automata, self-reproduction, the Garden of Eden and the game “life.” Scientific American, 224(2), 112–117.
- Gardner, M. (1970). Mathematical Games: The fantastic combinations of John Conway’s new solitaire game “life.” Scientific American, 223(4), 120–123.
- Haran, Brady. “Inventing Game of Life (John Conway),” Numberphile. March 3, 2014. Online interview. https://youtu.be/R9Plq-D1gEk.
- Hayles, N. K. (1999). How We Became Posthuman: Virtual Bodies in Cybernetics, Literature, and Informatics. University Of Chicago Press.
- Helmreich, S. (1998). Silicon Second Nature: Culturing Artificial Life in a Digital World. University of California Press.
- Milburn, C. (2008). Nanovision. Duke University Press.
- Milburn, C. (2018). Respawn. Duke University Press.
- Conway’s Game of Life viewer: https://copy.sh/life
- Rendell, Paul. “Universal Turing Machine in Conway’s Game of Life,” 10 February, 2010. Online. http://www.rendell-attic.org/gol/utm/index.htm
Discord Discussion
This discussion has been copied from the Discord server, names have been reduced to first name, discussion threads have been grouped and edited for better readability.